Casino House Odds
This reduces the difference between the true odds and casino odds to just 1 unit. So, using our house edge math we can calculate the edge as 1 x (1/37) = 0.027 or 2.7%. French Roulette. You're at a casino which offers you a 4 to 1 payoff if you bet on a single number on a roll of a six-sided die. The odds of winning are 5 to 1. You bet $1 every time, or a total of $6. On 5 of those rolls, you lose a dollar. The “house” would earn $3, or a 23 percent profit on your wagering. So just how long do you think you’d be able to keep playing at this rate? Each time you’re offered an arrangement similar to this in a casino game, the difference between the odds of the reduced payoff and the actual odds is known as “the house. Roulette odds There are two main versions of roulette, American and European, and both have their own particular set of odds. The house edge (the edge that a casino has over a player) on almost all.
- Casino Game Odds Chart
- Big Six
- Blackjack Casino Odds
- Which Casino Games Have The Best And Worst Odds?
- Best Odds Casino
Here’s the thing about casino games:
They’re all rigged.
But not in the way you think they are.
I had an interesting argument with a friend of mine the other night. He’s a conspiracy theorist, through and through. I mean, he believes the earth is flat (for real).
He’s absolutely convinced that the results of casino games aren’t random at all. He thinks all the games are rigged so that you can’t win. The only exception, according to him, is craps. He said that it’s impossible to rig a pair of dice.
I tried to explain to him that the casinos don’t need to cheat on the outcomes because they’ve set the payout odds up in such a way that they have a mathematical edge that no one can beat in the long run. They do this by offering payout odds that aren’t as good as the odds of winning.
For example, if you were playing roulette and betting on black, and that bet paid off at even money, you’d break even in the long run if you had a 50% chance of winning.
But you don’t have a 50% chance of winning that bet. You only have a 47.37% probability of winning that bet, because there are 38 numbers on the wheel, and only 18 of them are black—not 19.
The House Edge in Casino Games
Casinos, gamblers, and writers quantify this advantage that the house experiences with a percentage called “the house edge.”
It’s the long-term average percentage of each bet that the casino expects to win because of this discrepancy between the odds of winning and the payout odds.
For example, if I say that the house edge in roulette is 5.26%, it means that you can expect to lose an average of $5.26 every time you place a $100 bet on a roulette spin.
The higher the house edge is for a game, the worse the odds are for the player. The lower the house edge is, the better the odds are for the player.
And to make things even more confusing, many games offer multiple bets, each of which has a different house edge. Craps is a good example of this. Some of the bets at the craps table are among the best odds in the casino, but many of them have some of the worst odds in the casino.
This post focuses exclusively on the worst odds in the casino. Please don’t place these bets unless you just hate money and love casinos.
Also, don’t worry about whether the outcomes to the games are rigged. They’re not, for the simple reason that they don’t need to be. The casinos make more money by offering honest games. If the games’ outcomes were rigged, no one would play them.
1- Keno Has a House Edge Close to 30%
Keno is a simple game of number-picking that closely resembles the lottery. It is, in fact, a privately run lottery hosted by the casino with drawings every few minutes. You choose between 9 and 15 numbers from 80 potential numbers.
The casino draws 20 balls from that same pool of 80 numbers. If enough of your numbers match the numbers that the casino drew, you win a prize. The more matches you have, the more your payout is.

If you know anything about the lottery, you know that the house edge is close to 50%. Keno, being a similar game, has a similar house edge. But it’s actually a better game than the lottery, with a house edge that can vary between 20% and 40%. The average seems to hover around 30%.
Players like keno because they can stay in action relatively constantly without risking much money. They also enjoy the possibility of winning a huge cash prize. The only other games in the casino which offer such a potentially big return on your bet are the slot machines.
But that roughly 30% house edge makes keno the game with the worst odds in the casino. Most of the other bets on most of the other games don’t even come close.
2- The Logo or Joker Bet on the Big Six Wheel Has a House Edge of about 24%
The Big Six Wheel is such an old-fashioned casino game that it’s not even available in most casinos anymore. It resembles a carnival game more than anything else. All the bets on the Big Six Wheel are lousy, but a bet on the logo/joker is usually the worst bet.
Here’s how the Big Six Wheel works:
You have a vertical “wheel of fortune” with various dollar amounts on the wheel. Usually, you can bet on the following dollar amounts:
- $1
- $2
- $5
- $10
- $20
- The Joker
You bet a dollar on any of these amounts, and if the wheel lands on that amount, you win the prize. The probabilities of winning are, of course, determined by how many total stops are on the wheel and how many of those are the prize you bet on.
You might have 54 total stops on the wheel. If only one of those is the joker, then the probability of winning a bet on the joker is 1/54, or 53 to 1.
The payoff for that bet is usually 40 to 1.
That’s a huge discrepancy between your odds of winning and the payout for the bet, but what does it mean in terms of an average.
That’s easy to calculate, too.
Assume you bet $100 on 54 spins of the wheel, and assume you get statistically perfect results. You lose 53 times, for a total loss of $5300. You win once, for a total win of $4000. Your net loss is $1300.
Since you want an average loss per spin, you divide that net loss of $1300 by the 54 spins, and you find that you’ve lost an average of $24.07 per spin.
Since you were betting $100 per spin, you can say that the average loss is 24.07% of your bet.
That’s a huge house edge, making this bet an example of the 2nd worst odds in the casino.
The $5 bet and the $20 bet are almost as bad. The house edge on each of those is 22.22%.
Of course, some casinos have different versions of the Big Six Wheel with different prizes and different odds.
3- The 2-Face Domino Bet in Sic Bo Has a House Edge of 18.52%
Sic Bo is an Asian-themed dice game where you bet on the outcome of a roll of 3 dice. You can bet on various outcomes, like the total of the 3 dice, or whether the total is high or low. The house edge is high on almost all these bets, but the 2-face domino bet is usually the Sic Bo bet with the worst odds.
The 2-face domino bet is a wager on 2 specific numbers coming up on the dice. For example, you might place a 1-6 2-face domino bet. If one of the dice has a 1, while another has a 6, you win this bet.
If you place a 1-6 bet, any of the following outcomes would be winners:
- 1-6-1
- 1-6-2
- 1-6-3
- 1-6-4
- 1-6-5
- 1-6-6
It’s a horrible bet in the middle of a table full of mediocre and worse bets. The small and big bets are really the only Sic Bo bets worth making, and the house edge on those is 2.78%. That’s far from the worst in the casino, but that’s far and away the best bet on the Sic Bo table.
4- The Tie Bet in Casino War Has a House Edge of 18.65%
Casino War is one of the dumbest games in the casino. It’s literally just a gambling version of the kids’ game where you compare one card from each of you to see which one is higher. It’s also a lightning fast game, which means that you’ll lose more money faster because of the number of bets you’ll place per hour.
Most people just place a standard bet, which wins if the player’s card is higher than the dealer’s. It loses if the dealer’s card is higher. If there’s a tie, the player can surrender half his bet or go to war. If he goes to war, he places a 2nd bet, the dealer burns 3 cards, and then deals another card to both the player and herself. If the player then wins, he gets paid off, but only on that 2nd bet. The first bet is considered a push. If the player loses, he loses both bets.
It’s obvious where the house gets its edge in that situation, since the game would be 50/50 if the player didn’t have to place a 2nd bet for a chance to only win one unit.
But you also have the option to bet that the first 2 cards will tie. If you win that bet, the payoff is 10 to 1. The odds of a tie vary based on how many decks are in use. In a 6-deck game, the odds of a tie are about 12.5 to 1.
It’s silly to play Casino War to begin with.
But since the tie bet offers some of the worst odds in the casino, it’s even sillier to place that bet.
5- The “Any 7” Bet in Craps Has a House Edge of 16.67%
Some bets in craps are one-roll bets. The outcome of the next roll determines whether the bet wins or loses. The any 7 bet is one of these. It’s just a bet that the next roll of the dice will wind up with a total of 7.
This doesn’t sound like the worst bet in the world at first. After all, a 7 is the most likely total in craps. The odds of winning this bet are 5 to 1.
The problem is that the payoff for this bet is only 4 to 1.
Using the $100 bets on 6 perfect rolls of the dice method for calculating the house edge, you get the following results:
You lose $100 on 5 bets, for a total loss of $500. You win $400 on one bet, for a net loss of $100.
Divide $100 by 6 spins to get the average amount lost per roll, and you get $16.67.
Some of the bets at the craps table offer a house edge as low as 1.41%,
Why would you feel the need to place a bet where your average losses will be more than 10 times that?
Ignorance is the only excuse I can imagine.
6- Slot Machines Might Have a House Edge as High as 25%
Slot machines, unlike other casino games, make their house edge opaque. To calculate the house edge of a casino game, you need 2 pieces of information:
- The prize amount
- The probability of winning
On a slot machine, you have a list of prize amounts for the various reel combinations. It’s called the pay table.
What you lack are the probabilities of winning these prizes. It depends on the probability of getting any given symbol on the pay line, and that probability can be anything. The results on a slot machine spin are determined by a computer program called a random number generator (RNG).
It can be programmed to give one symbol a 1/10 probability, another symbol a 1/20 probability, and all the other symbols 1/8 probabilities. Or you could have an entirely different set of probabilities.
You can even have 2 slot machines with the same symbols and the same themes with entirely different probabilities attached to them. In other words, the machines might be identical on the surface, but one might have a house edge of 5% while the other has a house edge of 25%.
Most slot machines don’t have a house edge this high.
But it’s impossible for you to tell which slots have which house edge figures behind them.
Also, no other game in the casino plays as fast as slots. Remember how I said Casino War plays really fast? I was talking about 200 bets per hour, maybe.
But it’s not unusual to make 600 bets per hour on a slot machine.
My advice to savvy gamblers who like their money is to avoid slot machines as much as possible.
7- The 5-Number Bet in American Roulette Has a House Edge of 7.89%
Roulette odds are some of the most mediocre in the house. A standard bet on an American roulette wheel has a house edge of 5.26%.
But one bet on the American roulette wheel has the distinction of offering a house edge even worse than that.
This is the 5-number bet.
It’s a bet that the ball will land on any of the following results:
- 0
- 00
- 1
- 2
- 3
The probability of winning that bet is 5/38.
If you placed $100 bets on that bet for 38 spins, you’d win 5 times, and you’d lose 33 times. That’s a loss of $3300.
The payoff is 6 to 1, so you’ll win $600 on 5 of those bets, for winnings of $3000.
Your net loss is $300.
Averaged out over 38 spins, that’s $7.89 lost per spin or 7.89%.
Most people shouldn’t bet on any of the bets at the American roulette table, but placing this bet is just silly. You might as well give the casino your money and let them kick you in the stomach while you’re at it.
Conclusion
It’s always interesting to look at subjects like the worst odds in the casino. It’s also important to remember that from a certain perspective, it doesn’t really matter how good or bad the odds are. If the house has any edge, no matter how small, the casino will eventually win all your money. You just need to play long enough, and they’ve got you.
But from the perspective of getting value for your money, which bets offer the worst odds versus which bets offer the best odds is a crucial question. It helps you decide where to put your money to get the best chance for a lot of entertainment in the casino for your money.
If you’re losing $230/hour instead of $8/hour, you’re probably not getting as much entertainment for your money. Understanding which bets offer the worst odds is the first step in getting to that smaller hourly loss amount.
Introduction
The house edge is defined as the ratio of the average loss to the initial bet. In some games the beginning wager is not necessarily the ending wager. For example in blackjack, let it ride, and Caribbean stud poker, the player may increase their bet when the odds favor doing so. In these cases the additional money wagered is not figured into the denominator for the purpose of determining the house edge, thus increasing the measure of risk. For games like Ultimate Texas Hold 'Em and Crazy 4 Poker, where there are two required initial wagers, the house edge is based on one of them only. House edge figures are based on optimal or near-optimal player strategy.
The table below shows the house edge of most popular casino games and bets.
Casino Game House Edge
| Game | Bet/Rules | House Edge | Standard Deviation |
|---|---|---|---|
| Baccarat | Banker | 1.06% | 0.93 |
| Player | 1.24% | 0.95 | |
| Tie | 14.36% | 2.64 | |
| Big Six | $1 | 11.11% | 0.99 |
| $2 | 16.67% | 1.34 | |
| $5 | 22.22% | 2.02 | |
| $10 | 18.52% | 2.88 | |
| $20 | 22.22% | 3.97 | |
| Joker/Logo | 24.07% | 5.35 | |
| Bonus Six | No insurance | 10.42% | 5.79 |
| With insurance | 23.83% | 6.51 | |
| Blackjacka | Liberal Vegas rules | 0.28% | 1.15 |
| Caribbean Stud Poker | 5.22% | 2.24 | |
| Casino War | Go to war on ties | 2.88% | 1.05 |
| Surrender on ties | 3.70% | 0.94 | |
| Bet on tie | 18.65% | 8.32 | |
| Catch a Wave | 0.50% | d | |
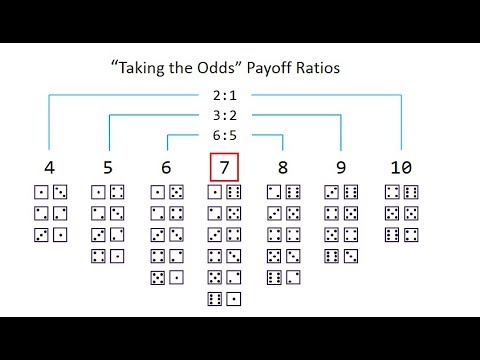
| Craps | Pass/Come | 1.41% | 1.00 |
| Don't pass/don't come | 1.36% | 0.99 | |
| Odds — 4 or 10 | 0.00% | 1.41 | |
| Odds — 5 or 9 | 0.00% | 1.22 | |
| Odds — 6 or 8 | 0.00% | 1.10 | |
| Field (2:1 on 12) | 5.56% | 1.08 | |
| Field (3:1 on 12) | 2.78% | 1.14 | |
| Any craps | 11.11% | 2.51 | |
| Big 6,8 | 9.09% | 1.00 | |
| Hard 4,10 | 11.11% | 2.51 | |
| Hard 6,8 | 9.09% | 2.87 | |
| Place 6,8 | 1.52% | 1.08 | |
| Place 5,9 | 4.00% | 1.18 | |
| Place 4,10 | 6.67% | 1.32 | |
| Place (to lose) 4,10 | 3.03% | 0.69 | |
| 2, 12, & all hard hops | 13.89% | 5.09 | |
| 3, 11, & all easy hops | 11.11% | 3.66 | |
| Any seven | 16.67% | 1.86 | |
| Crazy 4 Poker | Ante | 3.42%* | 3.13* |
| Double Down Stud | 2.67% | 2.97 | |
| Heads Up Hold 'Em | Blind pay table #1 (500-50-10-8-5) | 2.36% | 4.56 |
| Keno | 25%-29% | 1.30-46.04 | |
| Let it Ride | 3.51% | 5.17 | |
| Pai Gowc | 1.50% | 0.75 | |
| Pai Gow Pokerc | 1.46% | 0.75 | |
| Pick ’em Poker | 0% - 10% | 3.87 | |
| Red Dog | Six decks | 2.80% | 1.60 |
| Roulette | Single Zero | 2.70% | e |
| Double Zero | 5.26% | e | |
| Sic-Bo | 2.78%-33.33% | e | |
| Slot Machines | 2%-15%f | 8.74g | |
| Spanish 21 | Dealer hits soft 17 | 0.76% | d |
| Dealer stands on soft 17 | 0.40% | d | |
| Super Fun 21 | 0.94% | d | |
| Three Card Poker | Pairplus | 7.28% | 2.85 |
| Ante & play | 3.37% | 1.64 | |
| Ultimate Texas Hold 'Em | Ante | 2.19% | 4.94 |
| Video Poker | Jacks or Better (Full Pay) | 0.46% | 4.42 |
| Wild Hold ’em Fold ’em | 6.86% | d |
Notes
| a | Liberal Vegas Strip rules: Dealer stands on soft 17, player may double on any two cards, player may double after splitting, resplit aces, late surrender. |
| b | Las Vegas single deck rules are dealer hits on soft 17, player may double on any two cards, player may not double after splitting, one card to split aces, no surrender. |
| c | Assuming player plays the house way, playing one on one against dealer, and half of bets made are as banker. |
| d | Yet to be determined. |
| e | Standard deviation depends on bet made. |
| f | Slot machine range is based on available returns from a major manufacturer |
| g | Slot machine standard deviation based on just one machine. While this can vary, the standard deviation on slot machines are very high. |
Guide to House Edge
The reason that the house edge is relative to the original wager, not the average wager, is that it makes it easier for the player to estimate how much they will lose. For example if a player knows the house edge in blackjack is 0.6% he can assume that for every $10 wager original wager he makes he will lose 6 cents on the average. Most players are not going to know how much their average wager will be in games like blackjack relative to the original wager, thus any statistic based on the average wager would be difficult to apply to real life questions.
The conventional definition can be helpful for players determine how much it will cost them to play, given the information they already know. However the statistic is very biased as a measure of risk. In Caribbean stud poker, for example, the house edge is 5.22%, which is close to that of double zero roulette at 5.26%. However the ratio of average money lost to average money wagered in Caribbean stud is only 2.56%. The player only looking at the house edge may be indifferent between roulette and Caribbean stud poker, based only the house edge. If one wants to compare one game against another I believe it is better to look at the ratio of money lost to money wagered, which would show Caribbean stud poker to be a much better gamble than roulette.
Many other sources do not count ties in the house edge calculation, especially for the Don’t Pass bet in craps and the banker and player bets in baccarat. The rationale is that if a bet isn’t resolved then it should be ignored. I personally opt to include ties although I respect the other definition.
Element of Risk
For purposes of comparing one game to another I would like to propose a different measurement of risk, which I call the 'element of risk.' This measurement is defined as the average loss divided by total money bet. For bets in which the initial bet is always the final bet there would be no difference between this statistic and the house edge. Bets in which there is a difference are listed below.
Element of Risk
| Game | Bet | House Edge | Element of Risk |
|---|---|---|---|
| Blackjack | Atlantic City rules | 0.43% | 0.38% |
| Bonus 6 | No insurance | 10.42% | 5.41% |
| Bonus 6 | With insurance | 23.83% | 6.42% |
| Caribbean Stud Poker | 5.22% | 2.56% | |
| Casino War | Go to war on ties | 2.88% | 2.68% |
| Crazy 4 Poker | Standard rules | 3.42%* | 1.09% |
| Heads Up Hold 'Em | Pay Table #1 (500-50-10-8-5) | 2.36% | 0.64% |
| Double Down Stud | 2.67% | 2.13% | |
| Let it Ride | 3.51% | 2.85% | |
| Spanish 21 | Dealer hits soft 17 | 0.76% | 0.65% |
| Spanish 21 | Dealer stands on soft 17 | 0.40% | 0.30% |
| Three Card Poker | Ante & play | 3.37% | 2.01% |
| Ultimate Texas Hold 'Em | 2.19%* | 0.53% | |
| Wild Hold ’em Fold ’em | 6.86% | 3.23% |
Standard Deviation
The standard deviation is a measure of how volatile your bankroll will be playing a given game. This statistic is commonly used to calculate the probability that the end result of a session of a defined number of bets will be within certain bounds.
The standard deviation of the final result over n bets is the product of the standard deviation for one bet (see table) and the square root of the number of initial bets made in the session. This assumes that all bets made are of equal size. The probability that the session outcome will be within one standard deviation is 68.26%. The probability that the session outcome will be within two standard deviations is 95.46%. The probability that the session outcome will be within three standard deviations is 99.74%. The following table shows the probability that a session outcome will come within various numbers of standard deviations.
I realize that this explanation may not make much sense to someone who is not well versed in the basics of statistics. If this is the case I would recommend enriching yourself with a good introductory statistics book.
Standard Deviation
| Number | Probability |
|---|---|
| 0.25 | 0.1974 |
| 0.50 | 0.3830 |
| 0.75 | 0.5468 |
| 1.00 | 0.6826 |
| 1.25 | 0.7888 |
| 1.50 | 0.8664 |
| 1.75 | 0.9198 |
| 2.00 | 0.9546 |
| 2.25 | 0.9756 |
| 2.50 | 0.9876 |
| 2.75 | 0.9940 |
| 3.00 | 0.9974 |
| 3.25 | 0.9988 |
| 3.50 | 0.9996 |
| 3.75 | 0.9998 |
Hold
Although I do not mention hold percentages on my site the term is worth defining because it comes up a lot. The hold percentage is the ratio of chips the casino keeps to the total chips sold. This is generally measured over an entire shift. For example if blackjack table x takes in $1000 in the drop box and of the $1000 in chips sold the table keeps $300 of them (players walked away with the other $700) then the game's hold is 30%. If every player loses their entire purchase of chips then the hold will be 100%. It is possible for the hold to exceed 100% if players carry to the table chips purchased at another table. A mathematician alone can not determine the hold because it depends on how long the player will sit at the table and the same money circulates back and forth. There is a lot of confusion between the house edge and hold, especially among casino personnel.
Hands per Hour, House Edge for Comp Purposes
The following table shows the average hands per hour and the house edge for comp purposes various games. The house edge figures are higher than those above, because the above figures assume optimal strategy, and those below reflect player errors and average type of bet made. This table was given to me anonymously by an executive with a major Strip casino and is used for rating players.
Casino Game Odds Chart
Hands per Hour and Average House Edge
| Games | Hands/Hour | House Edge |
|---|---|---|
| Baccarat | 72 | 1.2% |
| Blackjack | 70 | 0.75% |
| Big Six | 10 | 15.53% |
| Craps | 48 | 1.58% |
| Car. Stud | 50 | 1.46% |
| Let It Ride | 52 | 2.4% |
| Mini-Baccarat | 72 | 1.2% |
| Midi-Baccarat | 72 | 1.2% |
| Pai Gow | 30 | 1.65% |
| Pai Pow Poker | 34 | 1.96% |
| Roulette | 38 | 5.26% |
| Single 0 Roulette | 35 | 2.59% |
| Casino War | 65 | 2.87% |
| Spanish 21 | 75 | 2.2% |
| Sic Bo | 45 | 8% |
| 3 Way Action | 70 | 2.2% |
Footnotes
Big Six
* — House edge based on Ante bet only as opposed to all mandatory wagers (for example the Blind in Ultimate Texas Hold 'Em and the Super Bonus in Crazy 4 Poker.
Blackjack Casino Odds
Translation
Which Casino Games Have The Best And Worst Odds?
A Spanish translation of this page is available at www.eldropbox.com.
Best Odds Casino
Written by: Michael Shackleford